Yield Curves
The module above has two yield curves generated by the three parameter bond price model. Initially they have the same settings, the slider positions can be changed to show how the curves are affected. The r0 parameter reflects an asymptotic maximal logarithmic rate. The rates shown are in traditional percent yield to maturity. Since these are yields to maturity, the whole curve is affected by each of the parameters.
The daily constant maturity yield curves for Treasury bonds can also be described with these parameters. The yields in these curves are generally computed using a model of yields to maturity adjusted to a constant maturity by interpolation. To test the zero coupon model, these yield curves which can be download to Mathematica in XLM format, were converted to zero coupon model prices by the following formula to calculate the fit in terms of the parameters {r0, r1, k}.
![]()
In the graph above the formula is inverted to calculate the rate from the bond price model.
![]()
For reference, the Treasury yield curves were fit to the bond price model parameters for the years since 2006. The Treasury has changed its methods over the years, and some of the change appears to show up in the parameters, {r1, k}. Currently the fits are quiet good for the long end maturities but there is some oscillation in the current Treasury data in short term yields, which may be due to artifact induced by interpolation. The bond price model may be a better method. For reference the parameter fits to data available from the Treasury are shown below.
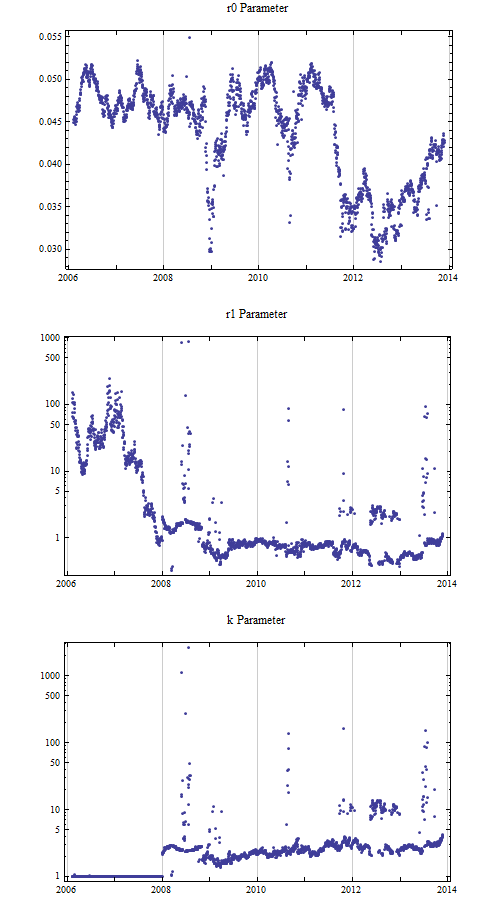
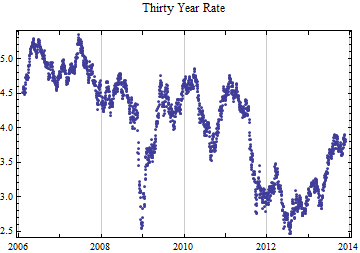
The pattern of the thirty year constant maturity rate is similar to the r0 parameter over the same time frame, but the r0 parameter currently is suggesting higher long term rates from the whole curve than the analysis of the thirty year bond by itself.
© Copyright 2013 Robert H. Rimmer, Jr. Thu 28 Nov 2013