Zero Coupon Model
Bond Price
The Bond Price graph, top left, shows the price of a zero coupon bond as a decimal fraction. The time on the graph is time to maturity, with zero being maturity time. At maturity, the bond value fraction equals 1, representing the full face value of the bond. At other times, the value is always less than 1. The plot has both a blue and red curve which are initially set to the same parameters, {r0, r1, k}, which are color matched to the curves. The two graphs can be compared to see how parameter changes affect the curves.
The value of r0 corresponds to the maximal logarithmic rate of growth from the point of view of decreasing maturity, this value is approached asymptotically on these graphs as t → ∞. But with a long time to maturity, this rate is very close to what is experienced while the log plot is linear. The decimal rate corresponding to r0 would be exp(r0) - 1. On the log price curves the negative of this rate is the slope of the linear portion of the curve.
The r1 and k parameters interact to create the bending of the curve as maturity is approached. r1 is set to be greater than r0. k is set in a range [0,8]. At k = 0 this becomes a pure exponential function and the rate on the yield curve will be a horizontal constant equivalent to Exp(r0)-1.
The tMax slider sets the extent of the curve from 1 to 30 years. It is easier to adjust the short end parameters when it has a shorter maximum time. Once they are set it can be opened up to show a larger curve.
The underlying function is a probability survival function, arising from the distribution of the sum of an exponential random variable with parameter, r0, and a gamma distribution random variable with a corresponding rate parameter, r1, and a parameter k. The gamma distribution parameters are set so that the gamma distribution represents a sum of k exponential random variables with rate r1. When k = 1, the whole distribution represents the sum of an r0 and an r1 exponential random variable. At k = 0, the gamma distribution component disappears and the price function becomes the survival function on an exponential distribution with rate, r0, i.e. p(t) = 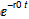 .
.
Log Plot Bond Price
This graph, bottom left, is the same plot as shown above it, but on a log scale. In this representation, when the curve is linear, the price is experiencing exponential growth with a logarithmic rate asymptotically close to r0, e.g. exp(r0 t), where t is time in years.
Yield Curve
This is a standard yield curve with decimal yields. All of the parameters interact, with the r0 having the greatest effect on the long end of the curve, while the r1 and k parameters control the shape of the shorter maturity end of the curve. The functions support curves with at most one inflection point.
First and Second Derivative Bond Price
First Derivative Plot, bottom right, represents the instantaneous rate of growth of the Bond Price curve. It is also a negative density function of the underlying probability distribution. It is always negative because for any given parameter set, the price is always declining as time to maturity is increasing. It reaches a maximal rate of growth at its negative mode after which the rate of growth slows to zero at maturity.
Second Derivative Plot, is the rate of change of the above plot on the same graph. It is positive when the first derivative is rising and negative when the first derivative is falling, it crosses zero at the nadir of the first derivative graph. When the function equals zero, it is the inflection point of the bond price curve, where the slope of the price stops rising and begins to fall. It is hard to see this point on the Bond Price plots but it is easy to see the zero crossing on this plot.
How to use this module
The program has two objectives, first to study how the parameters change the bond price function. But a more important use may be to simulate how the expectation of growth of a bond price will change after it is purchased. One way to set the parameters is to use the yield curve which is a more familiar shape, to set the parameters so that the yield curve has the desired shape.
Financial Data Analysis Home
© Copyright 2013 Robert H. Rimmer, Jr. Thu 5 Dec 2013