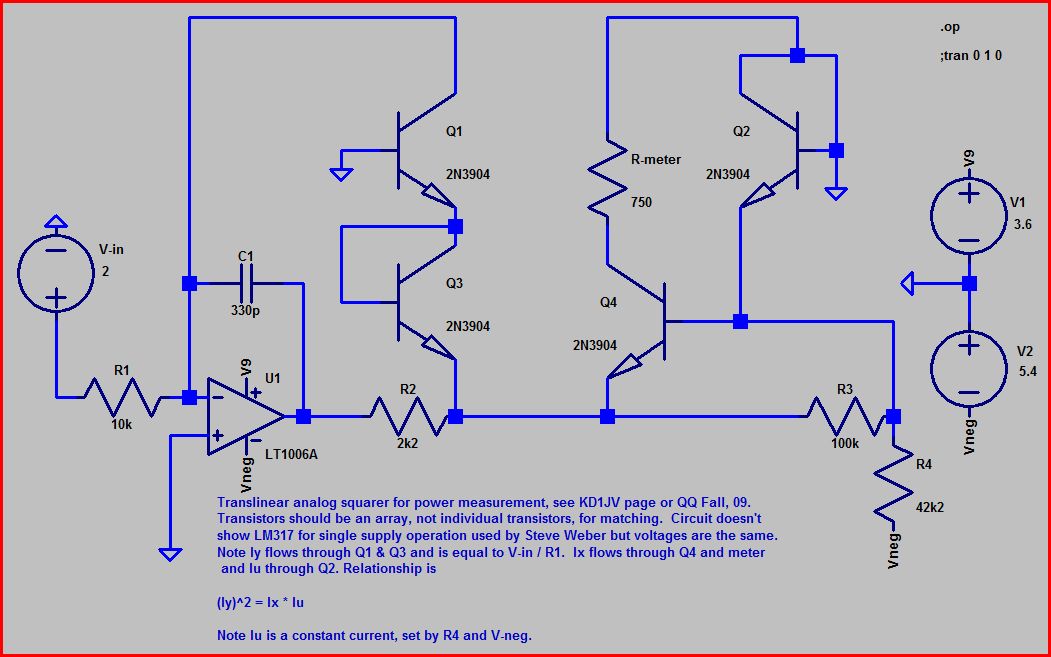
I’ve gotten really fascinated by the squaring circuit I originally saw on Steve Weber’s page and the description of the same circuit in QQ, where it is used to linearize a power meter circuit. It uses four transistors in a simple circuit with complex theory behind it, called translinear operation.

See http://en.wikipedia.org/wiki/Translinear_circuit for a discussion of the theory, named by Barrie Gilbert.

See http://kd1jv.qrpradio.com/lspwmtr/linear_analog_SWR_meter.HTM for Steve Weber’s circuit, which he based on a National Semiconductor app note. 

See also my LTSpice simulation for discussion.

The transistors need to be in a matched array since the relationship of current to Vbe, Is (saturation current), and temperature is critical. So a CA3046 array is used.  This keeps saturation currents and temperatures essentially equal among the transistors, eliminating error sources.

Steve designed for a single supply with a LM317L splitting a 9V battery to put about 3.6 volts on the positive pin of the IC and -5.4 volts on the negative.  First thing I did was build the regulator part (on prototype board) and verify these voltages.  Note that Steve’s pin numbers differ from the TO92 version of the LM317LZ regulator I used.

Some things to note about the circuit.  First, for the op-amp to be operating in a normal closed loop mode, it must be able to pull current from its inverting terminal equal to Vin / R1,  where R1 is 10k in our circuit.  This current flows through Q1 and Q3 in series.  Can the proper voltages be achieved to bias the transistors to do this?  Remember that the inverting terminal is a virtual ground so it’s at zero volts.  That means the grounded base of Q1 is electrically at the same potential as the collector.  So Q1 and Q3 are both virtually or actually connected base to collector.  To be “ON”, the collector / base junction must be about 0.6 VDC above the emitter for both transistors.  So the op-amp must go negative far enough to put the emitter of Q3 (and Q4) at about -1.2 volts.  So this is achievable and seen in reality and simulation.

Similarly on the right, Q4 and Q2 both have their collectors connected to ground (Q4’s collector goes through the meter to ground).  The emitter of Q4 is at the same ~ -1.2 VDC as that of Q2 and the emitter of Q2 has a path to negative voltage both through the b-e junction of Q4 and through R4.

I can’t derive the square-law relationship but I can state it from the wiki.  The pairs of transistors Q1/Q3 and Q2/Q4 form a translinear loop. First note that the emitters of Q2 and Q4 are common and so are the bases of Q1 and Q2.  Starting from the emitter of Q2 is a Kirchoff closed voltage loop going through the base-emitter junctions of Q3, Q1, Q2, and Q4.  Traveling around the loop in this way, Q3 and Q1 are called counter-clockwise elements as their emitters are oriented to the right and Q2 and Q4 are clockwise as their emitters point left (clockwise).  The law states that in such a loop, the product of currents in the clockwise loops is equal to the product of the currents in the CCW loops.  Amazing!  In this case CCW currents in Q1 and Q2 are equal and called Iy.  Current in Q4 is called Ix and current in Q2 is called Iu. 

So Iy is the measurement current (proportional to the input voltage), Ix is the meter current, and Iu is the scaling current.

A characteristic of this circuit is that Iu is a constant, programmed primarily by the value of R4 and the negative supply voltage.  So it is used for scaling.  The equation is

Iy * Iy = Ix * Iu

Since Iu is a constant, it can be seen that Ix is directly proportional to Iy squared.  So the current in the meter movement represents the square of the input current.  Which is directly proportional to the input voltage.  Therefore, the output current of the circuit represents the square of the input voltage.

BTW, I used an available op-amp from the LTSpice library, but my real physical circuit used a CA3140E, same as KD1JV used.

Sensitivity of the circuit to various resistors: 

R1 converts the input voltage to current and so sets the overall sensitivity of the circuit for a given power to voltage relationship from the RF input end.  To scale for higher power, R1 should be made larger.  For example, to double range of power, R1 should be 1.414 times larger. It’s assumed that a current transformer takes a sample of the transmitter output current, rectifies it and filters it to produce the voltage.  However it could also begin as a voltage sample scaled and rectified at the transmitter output.

I’m uncertain what R2 does for us.  The circuit is very insensitive to its value, with the output remaining constant as R2 changes from 2k2 to 1k5 to 100 ohms.  But with larger values, the op-amp has to output higher magnitude negative voltages.  If it reached the negative rail (-5.4 volts here), we’d be out of room.  Note that the current through this resistor is approximately Iy + Ix.

R3 will have some effect on accuracy or response as large changes affect the scaling current Iu.  It seems that R3 and R4 work together to program Iu although R4 has a greater effect.

R4:  Iu is approximately inversely proportional to the value of R4.  Changing it from 100k to 50k changed Iu from 50.6 uA to 94 uA.

R-meter – resistance of the meter had little effect.  Going from 100 ohms to 1000 ohms changed the meter current only 0.4% at full scale.

Also note that the voltage of the negative supply affects Iu.  Therefore, the regulator Steve Weber used not only allows single supply operation but also keeps the negative bus voltage constant with changing battery voltage.  The positive bus voltage will change, but it is not critical.

How to apply the circuit, roughly:

First decide or measure the input voltage at the desired 100% power level.  Say it’s 2 volts.  So the input current and Iy will equal 2/10k or 200 uA.  (I assume we’re using R1 = 10k for starters.)

Now what’s your meter movement’s full scale current?  Say it’s 350 uA. That’s Ix at full scale.  Now you can figure your Iu current from –

Iu = Iy^2 / Ix or in our case –

Iu = (200)^2 / 350 or 114.3 uA

I need to select R4 to produce that value of Iu.  By inspection, the current through R4 is approximately Iu – 6 uA and the voltage across R4 is Vneg – 0.6 volts.  So R4 is about

(5.4 V – 0.6 V) / (114.3 uA – 6 uA)  or 42.2 k-ohms.

In this simulation, this gave me a meter current of 332 uA versus 350 desired and an Iu current of 121 uA versus 114.3 required.  So R4 should be a pot which brackets the calculated value.  I would apply 2 volts to the input and adjust R4 for full scale on the meter to complete the calibration.